Author: Renaud Bédard

Fast .NET Reflection and Serialization

(sorry if you got this twice in your RSS, I hit the “publish” button too early…)

A while ago I decided to make an automatic serializer that works just like the XmlSerializer but for the SDL file format, since I like the simplicity and elegance of this data language. The XmlSerializer also doesn’t work natively with Dictionary objects, and crashes when used with certain visibility combinations and C# 3.0 auto-implemented properties.

Making a serializer for any language implies heavy use of reflection to determine the structure of what you’re reading or writing to or from a data file, but also to invoke the getter/setter of the fields you’re serializing.

Performance considerations

Some reflection operations come at a heavy performance cost. Not all of them though! This 2005 article in MSDN Magazine explains that fetching custom attributes, FieldInfo/PropertyInfo objects, invoking functions/properties and members and creating new instances are the costliest operations. Well that’s a problem, because all of those will be handy when writing our serializer.

The same article continues by showing which are the slowest method invocation techniques. The speediest technique are direct delegate use, virtual method calls or direct calls, but those are impossible to use if all you’ve got is a Type and an Object. The next best thing is using a DynamicMethod object, IL emission and a delegate. Having never used IL before, I didn’t grasp all of that, but thankfully there are many other resources concerning the use of DynamicMethod out there.

A post on Haibo Luo’s blog from 2005 makes a performance comparison between Activator.CreateInstance() (by the way, doing “new T()” with a generic type parameter that’s constrained as “new()” is the exact same as calling this method) and various other techniques including DynamicMethod and using it as a delegate. This last technique blows the rest out of the water in terms of speed.

This GPL library on CodeProject written by Alessandro Febretti provides an excellent dynamic method factory. And this other article on CodeProject goes a bit further and shows how to set/get values on fields, and isolates the boxing in helper functions.

What I ended up doing is taking from all of these examples, correcting the problems outlined in the comments of both CodeProject samples, and I built a IReflectionProvider interface that publishes all these costly operations and which can be implemented three different ways :

  • DirectReflector : Simply via reflection
  • EmitReflector : With IL emission but no caching performed (the DynamicMethods and delegates are rebuilt on each call)
  • CachedReflector : With IL emission and caching (the resulting delegates are created only once, then accessed with a dictionary lookup)

I’m aware that the 2nd test case is ridiculous, you should never emit IL and generate methods at runtime and repeatedly, but I wanted to outline the importance of caching.

The serializer

When making this sample, I wanted to both provide a fast .NET reflection library as well as a proper generic implementation of a reflective serializer. But I didn’t want to spend time on string parsing/formatting, since serializers usually output a text file or a certain data format. So the tradeoff I chose is somewhat unusable in the real world…

It outputs objects which are a generalization tentative of all .NET objects. There are three main categories :

  • SerializedAtoms are indivisible, single-valued and immutable. All primitive types will serialize to atoms, in addition to strings, enums and nullable types.
  • SerializedCollections are multi-valued object bags that don’t give a specific meaning to keys or indices other than natural ordering. All classes that implement ICollection<T> will serialize into this.
  • SerializedAggregates are multi-valued object maps that use the key or index for indentification. All of which doesn’t fall in the two other categories will serialize to aggregates, so Dictionaries and just any other class.

Only atoms contain actual values, but it contains them as an object. There is no string conversion done in the end, it all remains in memory. Serialized objects also retain the name of their host field or dictionary entry if any, and the runtime type if different from the declared one.

To customize the serialization output to an extent, I made a custom attribute called [Serialization] which allows to force an alternate name to a serialized member, mark a member as ignored by the serializer, or mark it as required. I could’ve used “optional” instead, but I find it more logical to skip serialization of all null or default-valued fields.

Just like the XmlSerializer, it only serializes the public instance fields or properties. So unlike the BinaryFormatter (which is deep serialization), my serializer does shallow serialization.

I have tested the implementation with many (if not all) combinations of value-type/class, serialized object category and visibility, so I can say it’s pretty robust and tolerant on what you feed it.

Results

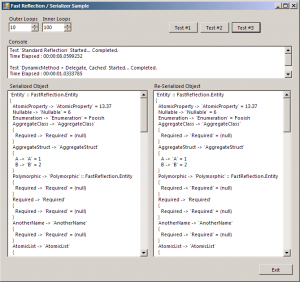
This is the whole point… how fast does “Fast .NET Reflection” go? Here are the timings for 10 outer loops (so 10 serializer creations) and 100 inner loops (100 serializations per outer loop), which means 1000 serializations or the same complex aggregate object.

Test ‘Standard Reflection’ Started… Completed.
Time Elapsed : 00:00:08.2473666

Test ‘Reflection.Emit + Delegate (No Caching)’ Started… Completed.
Time Elapsed : 00:01:52.4517968

Test ‘DynamicMethod + Delegate, Cached’ Started… Completed.
Time Elapsed : 00:00:00.9970487

Well, I did say that no caching was a very bad idea.

Still, the highlight here is that by running the same serialization code with two different reflection function providers, using dynamic IL methods and a healthy dose of caching is eight (8!) times faster than using standard reflection.

Sample code

The code for this sample (C# 3.5, VS.NET 2008) can be found here : FastReflection.zip (46 Kb)

Even if you’re not interested in serialization, I suggest you take a look at the EmitHelper class and how it’s used in CachedReflector. All tasks that need Reflection in a time-critical context should use dynamic methods!

Point Source Energy Decay

When playing with explosions, I was trying to determine how much an explosion’s energy or force is lost as you move away from the source. After Googling a bit, I found out that as per Coulomb’s Law (which relates more to electric forces, but makes sense for pretty much any point energy source), the energy is inversely proportional to the square of the distance. Kudos to Matthew for helping me find that information.

I intuitively knew that this made sense, probably seen it in other places… but I couldn’t explain it. Why 1 / d²?

After thinking a bit more about it, I managed to pull off a simple yet formal proof to this for any point energy source like sound and light… and explosions!

Circles on the water

You have to imagine an infinitely small, even null-sized energy source, like a point light in graphics programming. This point energy source emits energy in all directions equally. So let’s say it emits a single pulse at 0-time.

This source emits a 3D sphere around it, which is very dense and concentrated at first (infinitely dense at t=0) but the same energy spreads and becomes less and less dense. This energy “density” defines how much actually hits a surface or object at any distance.

The energy “particles” (that doesn’t sound right, but it’s conceptual) that form that expanding ring are traveling away from the center at constant speed, we’re assuming no friction or resistance in the surrounding medium. It’s a vacuum.

We know that the area of a sphere’s surface is 4πr², where r is the radius of that sphere. Let’s calculate its area at different times, considering that it grows in radius linearly through time :

t0 : r = 0, a = 0
t1 : r = 1, a = 4π
t2 : r = 2, a = 16π
t3 : r = 3, a = 36π
…
ti : r = i, a = 4πi

So, now that we know the area, I ask the question : How much “energy density” is contained in one square unit of that sphere’s surface at any given time?

Simply put, that’s the inverse of its area. Since we know that the entire area contains all the initial pulse’s energy, one square unit divided by this entire area corresponds to the amount of energy it contains.

And we want to remove all units here, so let’s calculate the ratio to the size at t=1. That gives… :

t0 : a’ = +∞, ratio = +∞
t1 : a’ = 1/4π, ratio = 1
t2 : a’ = 1/16π, ratio = 1/4
t3 : a’ = 1/36π, ratio = 1/9
…
ti : a’ = 1/4πi, ratio = 1/i²

There you have it. The amount of energy at time t and an equal distance, is the inverse of the square of that value. That is to say… 1 / d²!

I rest my case. :D

Loop Parallelism in a Game Context

An update to this post is available here.

Recently I was coding some physics-enabled particle systems and ended up with some fairly CPU-intensive stuff that looped as times as there are active particles in a system, and as many as there are active particle systems, each update cycle.

And it got choppy.

I don’t like choppy.

So I had three choices :

  • Offload to the GPU using GPGPU or Vertex Textures, but doing that in XNA with Shader Model 2 support is… time-consuming. Especially when you have no background work on the subject.
  • Profile and optimize my physics code, or switch to a physics package like Havok or Farseer, but I expect that would also take too much time.
  • Multithread using loop parallelism to use 100% of my CPU power instead of 50%! (I have a Core 2 Duo processor, and there’s more and more mainstream PCs with dual-, quad- and even octo-cores)

I ended up doing the latter because it was the simplest, and multithreading is rarely ever simple. But in some specific cases, it’s not much of a headache, really.

If your looped operation does not change the context of further loops, that is if every loop can be done in any order and individually without any write locking, it takes like 30 minutes to get it to work in C#, and with no concurrency problems. It’s like offloading static Web content to a different server, just a matter of routing to the right hardware.

Annoyances and interrogations

  • ParameterizedThreadStart is not generic. If you have to pass a context to your threaded operation, you have to cast it back to what it really is, at each iteration. It’s unnecessary and annoying… is it slow?
  • Once a thread dies, you can’t resurrect it. Correct me if I’m wrong, but FSM knows I’ve tried, and a thread that finished its execution cannot be re-run, even if its thread-start method is the same. You have to instantiate another. Does that affect performance…?

The problem with thread creation is that I create a lot of temporary threads. They live a single update cycle, and I instantiate one per particle system per update cycle, at about 60 cycles per second. It sounds like it could slow things down.

So I made a test!

Benchmark

The (fictional) situation is the following : in the middle of a game loop, you have to evaluate the 0th Order Modified Bessel Function Of The First Kind for some reason. And you need to do that for a large dataset, say 500 times per update cycle.

Actually, this kinda makes sense if you’re calculating weights for a very wide Kaiser filter, which I will probably cover later. I had code laying around, which is why I used the elegantly-named Bessel function.

So, this is slow, because it’s an integral. And so multi-threading would be beneficial. The different strategies are :

  • Single-Threading; it’s always good to know how slow it went before all optimization… if only for programmer ego.
  • Multi-Threading, using the ParameterizedThreadStart delegate, which means we’ll have to cast the Object to our real context type.
  • Multi-Threading, using a class-local, strongly-typed context and the (parameterless) ThreadStart delegate. This way we avoid the cast, and sacrifice a weird variable in the host class’ header.
  • Multi-Threading, using a generic Thread wrapper that does the strongly-typed context caching instead of laying it around. It’s basically a proxy for Thread with the context variable.
  • Multi-Threading, using a single “kept-alive” Thread that is started once for all update cycles, and that is forced into an artificial idle state between update cycles.

I hoped, even half-expected that these solutions would go from slowest to fastest. The last one was particularly interesting because it skipped all the thread instantiations and instead, relies on a Monitor and a sync-lock object to “wait” between two update cycles. It also produces much less garbage.

Results

Here’s the result for 500 update cycles, in which I update a 500-sized data-set, in Release mode, out of the IDE so without any debugging, and as little stuff as possible running in the background. I used a Stopwatch object to calculate these timings.

Test ‘Single-Threaded’ Started… Completed.
Time Elapsed : 27.8970399 s

Test ‘Multi-Threaded, ParameterizedThreadStart’ Started… Completed.
Time Elapsed : 18.1804179 s

Test ‘Multi-Threaded, Class-Local Context’ Started… Completed.
Time Elapsed : 19.5161083 s

Test ‘Multi-Threaded, Generic Context’ Started… Completed.
Time Elapsed : 20.2257278 s

Test ‘Multi-Threaded, Kept-Alive Thread’ Started… Completed.
Time Elapsed : 23.7845815 s

Of course, everything goes differently from what I expected. :P

The good news is, thread creation in .NET is very fast. No need to worry about that anymore. In fact, trying to circumvent that using a single kept-alive thread and monitor use makes it go almost 30% slower!

Also, casting the object context every iteration is faster than any other strongly-typed alternative. Unless the word “Object” in your code makes you want to shoot someone, it’s the best way to go. Kind of sad, that.

Here’s the C#3.0 (VS.NET 2008) test project : Loop Threading Performance (24 Kb)

Sorry again for the absolute absence of comments, it’s late and I don’t feel like it. D:

A Note On Debugging

One thing that’s slightly alarming and certainly worth mentioning, is that the performance in the IDE (with Debugging, but not necessarily in “Debug” mode) is hugely different.

In debugging, the “kept-alive” thread is almost always faster than all other strategies, by as much as 15%. This never replicates in the real-world. So kids, always test out of the IDE, or add the empty green arrow (Start Without Debugging, Ctrl+F5) in your Visual Studio toolbar!

Gaussian Blur Revisited, part two

First part can be found here.
An implementation of the concepts presented in this series can be found here.

The Perfect Sigma

The last post’s closing note was, how are we to find the “perfect” standard deviation for a fixed number of taps such that exactly 0% of light is lost. This means that the sum of all taps is exactly equal to 1.

It’s absolutely possible, but to find this exact σ with algebra and possibly calculus was a bit over my head. So I just “binary-searched” across the decimals until my Excel grid told me that as long as double-precision goes (15 significant numbers), I have ≈ 1 as the sum. I ended up with the following numbers :

  • 17-tap : 1.2086
  • 15-tap : 1.1402108
  • 13-tap : 1.067359295
  • 11-tap : 0.9890249035
  • 9-tap : 0.90372907227
  • 7-tap : 0.809171316279
  • 5-tap : 0.7013915463849

17-taps per pass, so basically 289 effective texture samples (actually 34…), and a standard deviation of 1.2?! This is what it looks like, original on right, blurred on left :


So my first thought was, “This can’t be right.”

Good Enough

In my first demo, I used a σ = 2.7 for 9 taps, and it didn’t look that bad.
So this got me thinking, how “boxy” can the Gaussian become for it to still look believable? Or, differently put, how much light can we lose before getting a Box-like filter?

To determine that, I needed a metric, a scale. I decided to use the Mean Difference, a.k.a. Average Deviation.
A Box filter does not vary, it’s constant, so its mean difference is always 0. By calculating how low my Gaussian approximations’ mean difference goes, one can find how similar it really is to a Box filter.

The upper limit (0% box-filter-similarity) would be the mean difference of a filter that loses no light at all, and the lower limit (100% similarity) would be equal to a box filter at (again) 15 significant decimal numbers.

So I fired up Excel and made those calculations. It turns out that at 0% lost light, the mean difference is not linear with the number of taps. In fact, the shape highly resembles a bell curve :

I fitted this curve to a 4th order polynomial (which seemed to fit best in the graph) and at most, I got a 0.74% similarity for 0% lost light, in a 9-tap filter. I’m not looking for something perfect since this metric will be used for visual comparison; the whole process is highly subjective.

Eye Exam

Time to test an implementation and determine how much similarity is too much to this blogger’s eye.
Here’s a fairly tiny 17×17 white square on a dark grey background, blurred with a 17-tap filter of varying σ and blown up 4 times with nearest-neighbour interpolation :

The percentage is my “box-likeness” or “box filter similarity” calculation described in the last section.

Up to 50%, I’m quite pleased with the results. The blurred halo feels very round and neat, with no box limit that cuts off the values harshly. But at 75%, it starts to look seriously boxy. In fact, anything bigger than 60% visibly cuts the blur off. And at 100%, it definitely doesn’t look like a Gaussian, more like a star with a boxy, diamond-shaped blur.

Here’s how 60% and 100% respectively look at a 9-tap, for comparison :

50% looks a liiiiiitle bit rounder, but 60% is still very acceptable and provide a nice blurring capability boost.

Conclusion

My conclusion, like my analysis, is extremely subjective…
I recommend not using more than 60% box-similarity (as calculated with my approach) to keep a good-looking Gaussian blur, and not more than 50% if your scene has very sharp contrasts/angles and you want optimal image quality.

The ideal case of 0% lost light is numerically perfect, but really unpractical in the real world. It feels like a waste of GPU cycles, and I don’t see any reason to limit ourselves to such low σ values.

Here’s a list of 50% and 60% standard deviations for all the tap counts that I consider practical for real-time shaders :

  • 17-tap : 3.66 – 4.95
  • 15-tap : 2.85 – 3.34
  • 13-tap : 2.49 – 2.95
  • 11-tap : 2.18 – 2.54
  • 9-tap : 1.8 – 2.12
  • 7-tap : 1.55 – 1.78
  • 5-tap : 1.35 – 1.54

And last but not least, the Excel document (made with 2007 but saved as 2003 format) that I used to make this article : Gaussian Blur.xls

I hope you’ll find this useful! Me, I think I’m done with the Gaussian. :D

Gaussian Blur Revisited, part one

Second part can be found here.
An implementation of the concepts presented in this series can be found here.

A long time ago, in a blog not so far away, I studied how the Gaussian distribution worked to implement a Gaussian Blur HLSL shader. That worked pretty well, I learned a lot of stuff, and managed to make a very functional shader. But some problems were overlooked and fixed with not-so-scientific solutions/hacks. Last week and this week, I spent more time thinking and experimenting with Gaussian blur weights, and discovered some pretty interesting stuff.

Losing Light

The first problem that I mention in my original post is the fact that when passing any image through a Gaussian blur shader darkens it, a certain portion of brightness or “light” is lost in the process.
Usually, the Gaussian function (a.k.a. the bell curve or normal distribution) has an integral between from x = -∞ to +∞ of exactly 1. But when you sample it at discrete intervals, you always lose a certain portion of that full integral.
To prevent this effect, I decided to “normalize” all the weights (a weight being a sample of the G(x) function at some x distance) to have a sum of exactly one, since that’s what I want to end up with anyway. This works, and my filtered images are bright again.
But doing so has a subtle yet perverse effect to it.

Boxing the Gaussian

Let’s take a 5-tap uni-dimensional kernel with a standard deviation of σ = 1. As a reminder, the standard deviation defines how wide the function is, and how much blurring is performed, and the “tap” count is the number of texture samples done in a single pass (each pass being either horizontal or vertical).
Here are the weights acquired from the function, then the normalized weights (since the function is reflective at x = 0, I only show values for [0, 2]) :

0.39894228, 0.241970725, 0.053990967
Σ = 0.990865662

0.402619947, 0.244201342, 0.054488685
Σ = 1

That looks quite fine. Now let’s use a wider σ of 5.

0.079788456, 0.078208539, 0.073654028
Σ = 0.38351359

0.208045968, 0.203926382, 0.192050634
Σ = 1

Notice how the normalized weights are very close to each other. In fact, it highly resembles an averaging 5-tap Box filter :

0.2, 0.2, 0.2
Σ = 1

When you think about it’s it very natural for this effect to occur. The bigger the standard deviation, the closer to the curve’s apex you sample values, and the lower the apex as well. So the difference between the samples is smaller and you go closer to a straight line.
In fact, at σ = ∞, any normalized Gaussian kernel becomes a Box filter. I don’t have a formal proof for that, but it’s clearly visible, and with single-precision floats it takes a lot less than the infinity.

Visual Difference

Now why is it so bad to use a box filter? It’s as wide as our kernel can get with its limited number of taps after all…

Here’s a visual comparison of the same scene under a 5-tap Box filter and a Gaussian with σ ≈ 1.5, giving it about the same span. It’s not an apples-to-apples comparison, but it should give you an idea.

Comparison shot 1

Comparison shot 2

A Box filter is quite unlike a Gaussian blur. Sharp edges get blocky and it gives a more “sharp” feel than the Gaussian. So it’s definitely not optimal.

Ye Olde Cliffhanger

Getting late here, so I’ll wrap this up.
The question left is this one : At which standard deviation does our Gaussian sampling lose 0% brightness/light for a fixed number of taps? Is that even possible?
Why, yes, yes it is. I’ll keep this for part two!

Hash tables and mutable keys, final

I am really, really sick of seeing the preceding post and its cliffhanger on my blog’s front page, so here’s an abrupt end to it.

There is no sample/code, there won’t be any sample. But I do have one conclusion : If your algorithm needs a hash table with mutable keys, then don’t mutate their hash code.

There is absolutely no good reason for a hash set to have keys that get lost, and no point in hacking the data structure to trace all those swaps and recover from them.

Why do I say this after two lengthy posts about how to circumvent the problem? Simple. A hash set should be, first and foremost, a set. And sets are built upon the idea that all its elements are unique and there are no possible duplicates. But if an element can mutate enough to modify what uniquely identifies it, the operation potentially breaks this assumption. How can you know if your set has unique elements if the elements keep changing, and you can’t keep them from changing?

This leads me to the inevitable (yet predictable) conclusion that mutating keys is not a good idea. In my tests and situations, and I’ve tried for weeks to find a test case where sets mutable keys are absolutely needed, there is always a way around it, and it’s safer, it makes more sense.

So next time you see exceptions or problems of that nature (e.g. unreachable elements), think for a minute. Do you really need mutable keys? You probably don’t, but what if you do? Just don’t override GetHashCode() and move to something else.

There, problem solved. Moving on. :)

Hash tables and mutable keys, part two

(Part one is here.)

You know, I was so confident when writing the first post that I was addressing a common problem (which is not entirely untrue considering Google hits) and that it would be a pretty straightforward “here’s the issue, here’s the fix, enjoy” scenario.

Boy, was I wrong.

The common approach when trying to fix a bug is to first reproduce the problem. While I had no difficulty making a fictitious test case that does reproduce the “unreachable hashed entry” issue, I’m having all the trouble in the world finding a proper, real-world, justifiable algorithm that needs a hash table with mutable keys.
It just never seems to me like a reasonable thing to do.

Nevertheless, being the stubborn bastard that I am, I’ll present here a recipe to encounter the problem with as much justifications as I could make up. And if ever you’re ever stuck in a situation where you do need a hash set to react properly with mutable entries, well you’ll have a solution of sorts.

Take a deep breath (this is a looooong one) and hit the jump.

Continue reading Hash tables and mutable keys, part two

Hash tables and mutable keys, part one

In this little series of posts (probably two three), I’m going to address a problem that has happened to me yesterday and was a real blocker in my algorithm : how to get a hash table (HashSet or Dictionary) to work with keys that change their hash code over time.

Continue reading Hash tables and mutable keys, part one

Effect Compiler & Disassembler

Updated! Now supports nVidia’s ShaderPerf tool.

Downloads

EffectCompiler.zip [51.3kb] – XNA Game Studio Express 2.0 (Visual C# 2005 Express), Source + Binaries

Description

Yesterday I took apart my Effect Compiling Tool which took a HLSL shader and converted it to Windows/Xbox360 bytecode, and made it into something more useful outside of XNA.

It’s always been somewhat of a hassle for me to compile and disassemble HLSL shaders. I can edit them pretty well in Visual Studio with code coloring and tabulations/undo’s/whatnot, but to compile them I always had to go with something else. I had read in the book Programming Vertex and Pixel Shaders by W.Engel how to compile them in VC++ 2005 using a Custom Build Step and fxc.exe, but when working in C# I had to have a parallel C++ project just for shaders, which is dumb. Also, fxc.exe has become less and less stable for some reason… So I finally made my own compiler and disassembler using XNA 2.0.

Continue reading Effect Compiler & Disassembler

16-Bit Color Encoding on the GPU

While working on some tangent project you’ll know about pretty soon, I’ve been trying to pack color data that had little visual importance from 24-bit “Truecolor” R8G8B8 to 16-bit “Highcolor” R5G6B5. Intuitively the solution is to take the most significant bits of each component and fit it inside two 8-bit containers by using bitwise operations.

But the problem is, bitshifting and just any bitwise operator are not supported in shaders before SM4.0, and I am still lagging behind with my videocard and OS so I can’t run those yet. And anyway, I assume 95% of the world can’t either.
So the only way to make this is to resort to integer arithmetic (division, multiplication and modulus). And since it took me most of the day to have it working, I thought I’d share my little HLSL snippet with the world.

Update : Now with 232.3% less arithmetic instructions!
Update #2 : Added in netics’s optimization in the encoding, 3 less instructions!

float2 EncodeR5G6B5(float3 rgb24)
{
	// scale up to 8-bit
	rgb24 *= 255.0f;

	// remove the 3 LSB of red and blue, and the 2 LSB of green
	int3 rgb16 = rgb24 / int3(8, 4, 8);

	// split the green at bit 3 (we'll keep the 6 bits around the split)
	float greenSplit = rgb16.g / 8.0f;

	// pack it up (capital G's are MSB, the rest are LSB)
	float2 packed;
	packed.x = rgb16.r * 8 + floor(greenSplit);		// rrrrrGGG
	packed.y = frac(greenSplit) * 256 + rgb16.b;		// gggbbbbb

	// scale down and return
	packed /= 255.0f;
	return packed;
}

float3 DecodeR5G6B5(float2 packed) {
	// scale up to 8-bit
	packed *= 255.0f;

	// round and split the packed bits
	float2 split = round(packed) / 8;	// first component at bit 3
	split.y /= 4;				// second component at bit 5

	// unpack (obfuscated yet optimized crap follows)
	float3 rgb16 = 0.0f.rrr;
	rgb16.gb = frac(split) * 256;
	rgb16.rg += floor(split) * 4;
	rgb16.r *= 2;

	// scale down and return
	rgb16 /= 255.0f;
	return rgb16;
}

Update Notes : Now, the first version I had posted here was much more high-level, and used functions like rightShift(x, a) that emulated bitwise operators. The idea was good, and it allowed me to experiment until I got it working, but it was way too complicated and the HLSL compiler just couldn’t optimize it well enough. So I rewrote it.

The new version consumes 28 vs_3_0 instructions to encode, and 11 ps_3_0 instructions to decode including the texture sampling. The old one was respectively 69 and 24 instructions for the exact same result. It’s crazy how optimizable some tasks are.
The big changes were the caching of divisions in a variable and the use of floor() or frac() instead of integer arithmetic, packing of similarly used data in vectors to group operations, removal of all pow() function calls, and overall code tidying. It gives a pretty hard to understand decoding function, but >200% speed-up totally justifies it.

An additional thing that I found out while optimizing, it’s just impossible to remove most-significant-bits by left-shifting and right-shifting back into place with integer arithmetic. The reason is that there is no native integer math on GPUs before SM4.0 and even if you can push a number by 30-something bits, you can’t bring it back down because the inverse has too many decimals and the floats run out of them. So the natural way to work around that is right-shifting (divide by 2^x), then use of the frac() intrinsic, and left-shifting if necessary to bring it back up.

EncodeR5G6B5() and DecodeR5G6B5() take respectively one float3 and compresses it to float2, or the inverse. Most of the color information is kept because only 3 bits at most are stripped, and they’re in the 1-4 range.

The encoding logic is the following :

  • Take the float3 (24-bit) color and expand it to 256-base range.
  • Remove the least significant bits (3-2-3) of each components by using 2^x integer division.
  • Shift the 5-bit red component leftmost and place it in the first 8-bit field.
  • Split the 6-bit green component in the two fields; the three least significant bits (LSB) of the first field will have the component’s three most significant bits (MSB), and the three MSB of the second field will have the rest (the component’s three LSB). This might have sounded confusing, but basically we’re filling the holes in sequence.
  • Append the 5-bit blue component to the remaining space, no need to shift, just bitwise-OR it up.
  • Take back the range to 1-base by floating-point-dividing on 255.

The decoding logic is, as one would expect, the inverse.
One important mention though is the presence of the round intrinsic function. Without it, for reasons unknown to my sleep-deprived brain, I keep losing random bits. I assume that integer casting (explicit or implicit) in HLSL just drops all decimals, like a floor operation would, and to be consequent we need to round it off to the nearest integer.
And of course since we’re dealing with encoded data, any bit could make a dramatic change!

And as a closing note, it doesn’t work very well with FSAA or probably any sort of blending, because those change the intensities by arbitrary factors and will screw up the encoding. I’ve had problems with FSAA, haven’t tried blending yet but it would be expected behaviour.

Enjoy!