Update (Oct. 26th) : Better interpolation = better shaping, and the simpler “inscribed square” method.
Update (Nov. 4th) : Exact and customizable solution!
The input values of thumbsticks on an Xbox 360 controller are always contained inside the unit circle, a disk centered on the origin and whose radius is 1. This is usually fine, because you want to interpret the values as a vector inside that circle… but if you want to provide an analog version of a D-Pad, for instance to control a character in a 2D platformer, then you’ll find that your character will never reach maximum horizontal speed unless you hit the (1, 0) or (-1, 0) vectors, exactly right or left. Anything tilted up or down will give a fractional speed, and if you hit a diagonal corner, you’ll end up with ±√½.
So what if the analog stick was a square area instead, such that the entire circumference has a least one component maxed out, like the contour of a square?
It may seem like a simple thing to do, but it proved to be a lot of trouble, and in the end I chose to use an approximation (nope, it worked out in the end!)… but here’s how I researched the problem.
Attempt #1 : Wrong way around
I first googled “Mapping circle to square“, and ended up on a blog entry that describes the inverse transform. Fine, I’ll just invert it, isolate the x and y variables as a function of x’ and y’… But that proved to be a problem.
Wolfram|Alpha doesn’t know what to do with it, and after making it more manageable (for x, for y), it gives 4 different answers that seem to work only for specific intervals, but doesn’t say which…
I tried doing it by hand and was stuck early on, because I suck at this.
And since I don’t have access to (nor know how to use) proper nonlinear equation solvers, I decided to give up.
Attempt #2 : Projections
By googling some more and varying search terms, I stumbled upon a cool flicker image titled “Conformal Transformation: from Circle to Square“. That’s exactly what I need!
But alas, it involves something called elliptic integrals and this also goes beyond my math understanding, or the amount of effort I was willing to put in this. The description also links to the Peirce quincuncial projection, which maps a sphere to a square, but the math also goes above my head (complex numbers arithmetic and again, elliptic integrals).
At this point I realized that what I was trying to do was not trivial.
Attempt #3 : Intuition serves best
So I just went back what I usually do : analyze the problem, determine what I expect as a basic solution, and work my way there.
- Problem : The smallest horizontal component I end up with is ±√½, or ±~0.707, when the θ angle is π/4, 3π/4, 5π/4 or 7π/4.
- Solution : Scale this to ±1, so by a factor of √2.
The scale for angles close to diagonals should fall down to identity (1) when it reaches a cardinal direction, though I’m not sure about the interpolation curve… Linear should do fine?
(code removed because it’s kinda shitty)
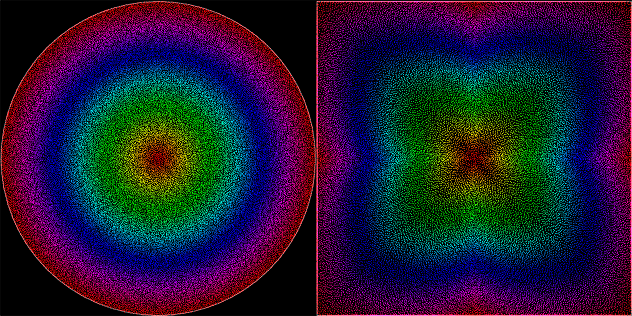
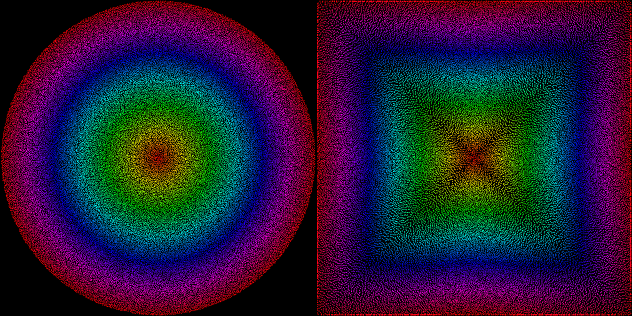
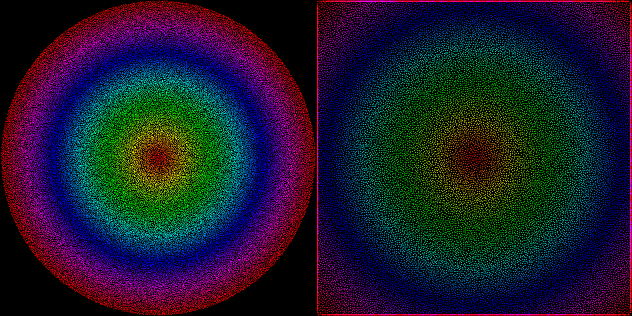
And for additional fun and testing, here’s how evenly-spaced random points inside the unit disk stretch to the unit square using this function (points generated by my Uniform Poisson-Disk code) :
Not bad? Good enough for me.
Attempt #4 : Interpolation and variations
I then tried different interpolation/easing methods for the scaling factor, and tried raigan’s idea of just scaling and clamping linearly the circle to a square, here’s what it looks like!
I tried sine, quadratic and circular ease in/out/in-out from my easing functions library, and quadratic ease-in was the most balanced. It almost shapes everything to a square, very little clamping is necessary, so I’ll keep that in.
The inscribed square method is nice and simple, but cuts off a lot of values and keeps circular gradients in its area. But in the real world, for 2D platformer input, it’s probably just fine…
Attempt #5 : Epic win
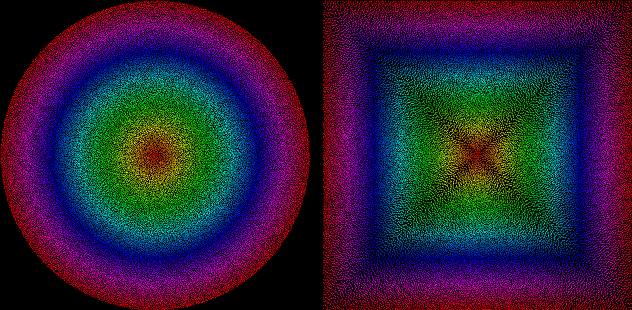
So, I decided to give another shot at this after speaking on the bus with a friend about polar coordinates and trigonometry. Turns out there is a more exact solution, and by adding a “inner roundness” parameter you can also tweak how much of the center input will remain circular, while still touching the sides for circumference values.
Here is my final C# function, then I’ll explain how it works :
static Vector2 CircleToSquare(Vector2 point)
{
return CircleToSquare(point, 0);
}
static Vector2 CircleToSquare(Vector2 point, double innerRoundness)
{
const float PiOverFour = MathHelper.Pi / 4;
// Determine the theta angle
var angle = Math.Atan2(point.Y, point.X) + MathHelper.Pi;
Vector2 squared;
// Scale according to which wall we're clamping to
// X+ wall
if (angle <= PiOverFour || angle > 7 * PiOverFour)
squared = point * (float)(1 / Math.Cos(angle));
// Y+ wall
else if (angle > PiOverFour && angle <= 3 * PiOverFour)
squared = point * (float)(1 / Math.Sin(angle));
// X- wall
else if (angle > 3 * PiOverFour && angle <= 5 * PiOverFour)
squared = point * (float)(-1 / Math.Cos(angle));
// Y- wall
else if (angle > 5 * PiOverFour && angle <= 7 * PiOverFour)
squared = point * (float)(-1 / Math.Sin(angle));
else throw new InvalidOperationException("Invalid angle...?");
// Early-out for a perfect square output
if (innerRoundness == 0)
return squared;
// Find the inner-roundness scaling factor and LERP
var length = point.Length();
var factor = (float) Math.Pow(length, innerRoundness);
return Vector2.Lerp(point, squared, factor);
}
There are two concepts here :
- The scaling factor can be calculated for every theta angle without any need for interpolation. It happens to be the inverse of the sine or cosine of the angle, depending on which wall you’re trying to clamp to. This gives a perfect square all around.
- By interpolating relatively to the length of the input vector, it’s possible to preserve the circular shape in the center and still clamp to the sides for extreme inputs.
I think I’m done with this now! Yay.

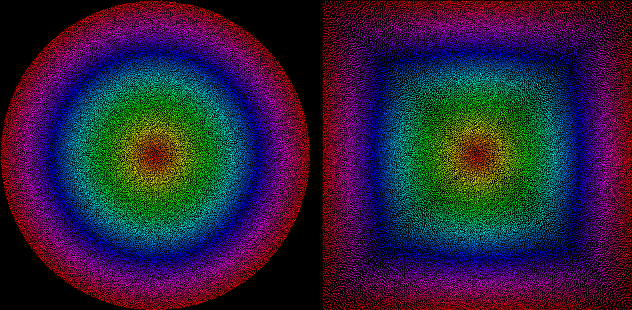
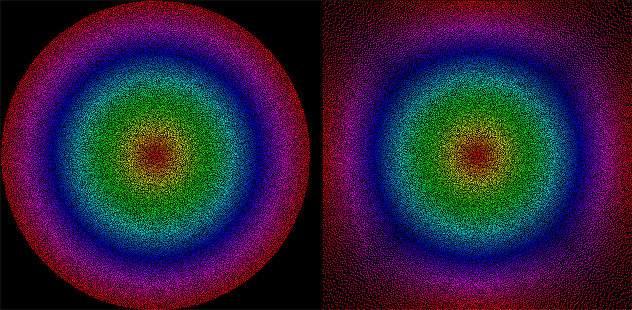
Glad to hear you figured it out!
Or there’s the lazy solution: inscribe a square in the circle, anything outside of the square gets clamped to the surface of the square (i.e to max value). Good enough :)
That’s just boring ;)
But it’s probably fine for thumbsticks, yup. Good to know.
N+ XBLA uses an even simpler method — no analog control, the thumbsticks are just thresholded to 0 or 1.
One thing is bugging me about the code: you have MathHelper.PiOver2 but no MathHelper.SqrtOf2 :p
Hehe, MathHelper isn’t my class, it’s part of the XNA framework. I actually have a MathHelperEx.Sqrt2 in my own libraries, but one may choose to just use a local const field or whatever.
Yeah, that sort of thing really bugs me.. stupid XNA :)
Hmm.. I may have misunderstood the goal of this exercise :)
Can I modify my suggestion? Once you clamp the input to within the inscribed square, you’d then want to interpret the input in the context of the square. I don’t really know what that last part means, I guess it would just be calculating the distance from the input position to the square’s edges — it should be just like bilinear interpolation.
..basically since you have a perfect square, it should be possible to produce and output that’s a perfect square gradient, instead of that clipped-circular gradient that’s currently being produced.
One way to do that would be to bilinearly interpolate between (1,1),(1,-1),(-1,-1),(-1,1) (i.e the four corners of the square) based on the current input position within the square.
I hope this makes sense!
I’m still not sure what you meant, because… the input values are inside a circle, I have to scale them by something to get the square values. And interpolation is still an approximation, based on what I tried. (unless you mean some other kind of interpolation)
But anyway, I figured out what I think is a perfect and flexible solution, see the update notes!
Yeah, actually I don’t think what I was thinking of could work, I just tried to write it out and it would still produce circular patterns :(
Nice that you found a solution though!
Congratulation Renaud!:)
Squaring The Thumbsticks | The Instruction Limit
This was SUPER helpful (exact solution) to a problem I was having with the Steam Controller trackpad. Thanks so much for posting it!
Glad it helped! :)
I came across this post all those years ago thinking that the people at Logitech, or third part app may do something similar for “newer” generation xinput controllers to make thumbsticks with circular holes work good for older dinput games which need square co-ordinates otherwise the movement is limited.
Has there been any app that in recent years that would do something similar? I’ve tried Steams settings inside of Big Picture but they never worked. Stuck using a Logitech F710 to control things like GTA:SA(non definitive) driving and flying very badly. GTA:SA mods that supposedly add xinput don’t seem to take this problem into account.